로피탈의 법칙은 특히 미분과 극한을 다룰 때 미적분학에서 중요한 도구입니다. 이 정리는 함수의 극한을 찾을 때 발생할 수 있는 불확정성 문제를 해결하는 데 도움이 됩니다. 로피탈 정리의 정의
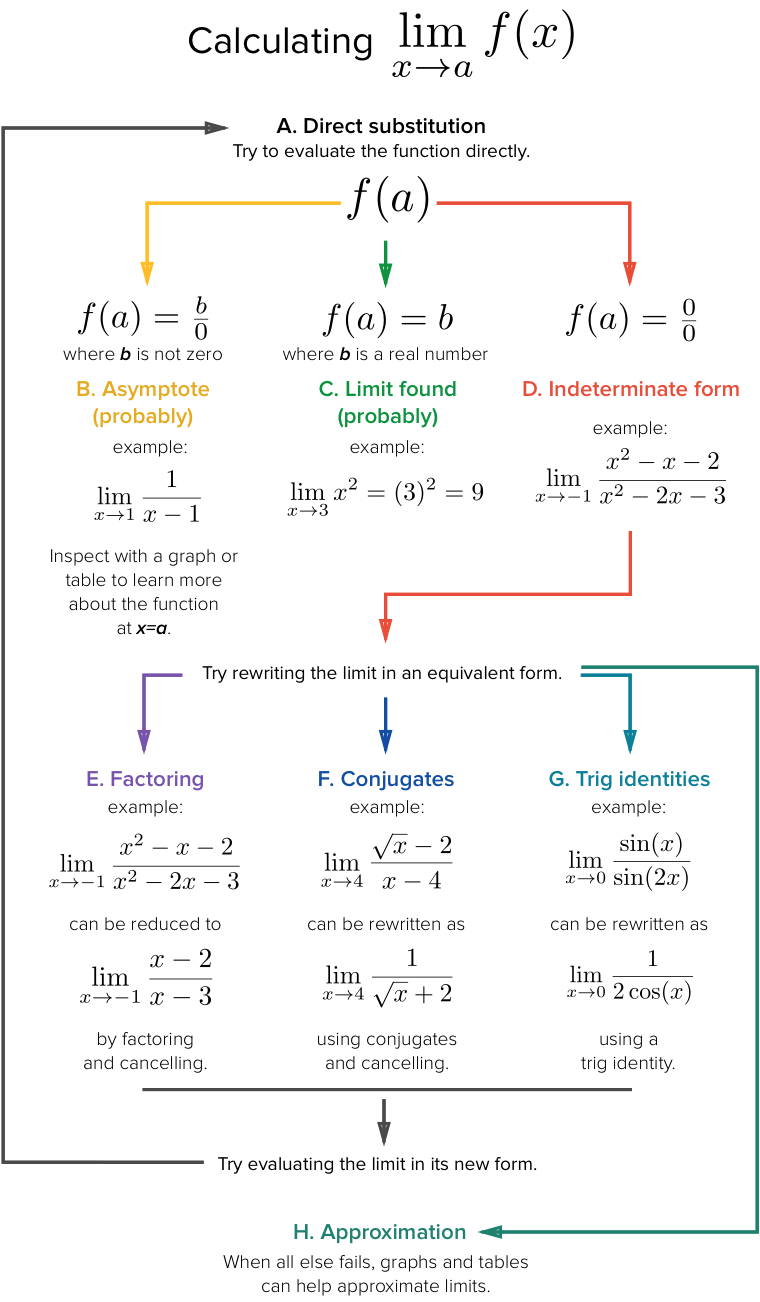
로피탈의 정리(L’Hopital’s theorem)는 극한을 계산할 때 불규칙한 형태(frac{0}{0}) 또는 (frac{infty}{infty})가 발생할 때 극한을 계산하는 방법을 제공합니다. 이때, 분자와 분모를 미분한 후 다시 극한을 구하는 방법이다. 로피탈 정리의 공식은 다음과 같습니다: (lim_{x to a} frac{f(x)}{g(x)} = lim_{ x to a} frac{f'(x)}{g'( x)})여기서:- ( f(x) ) 및 ( g(x) )는 ( x = a )에서 미분 가능한 함수여야 합니다.- ( lim_{x에서 a} f( 0으로 수렴할 때 또는 무한대에서는 분자와 분모를 따로 미분하여 다시 극한값을 구합니다.
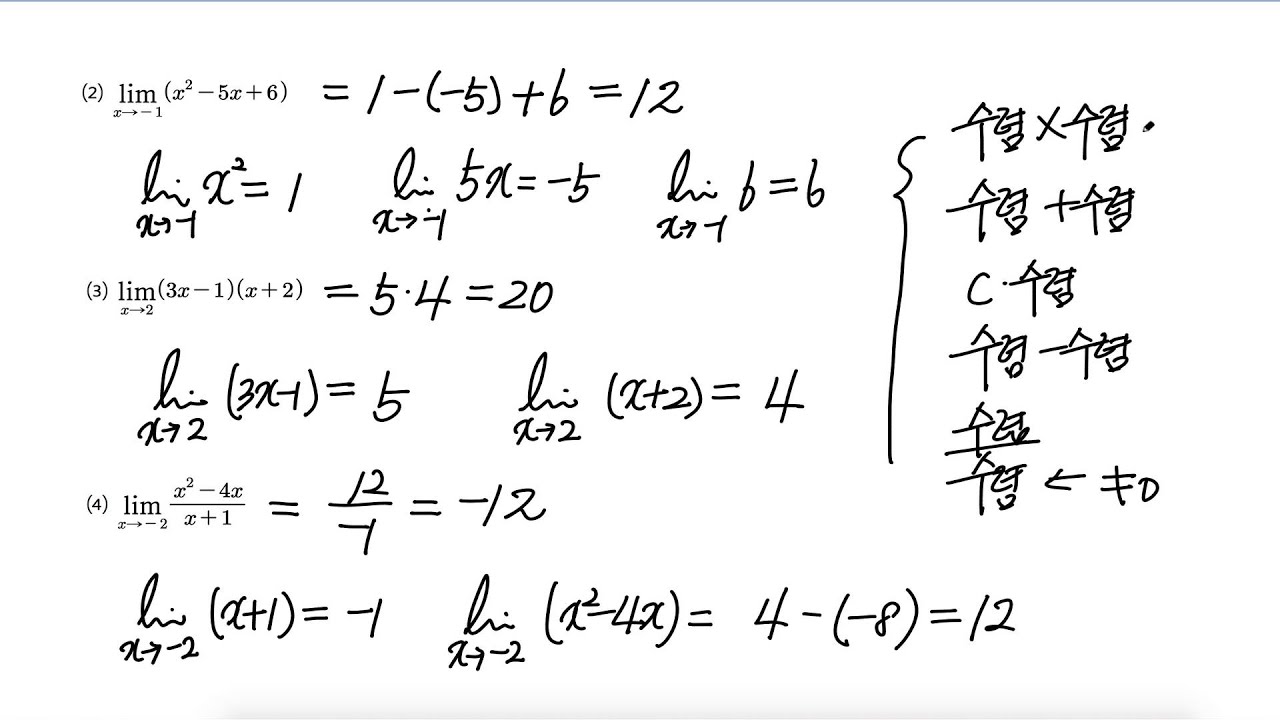
로피탈 정리의 적용 조건
1. 불확정 형태: 로피탈의 정리는 0/0이나 무한대/무한과 같은 불확정 형태를 가질 때 극한을 구하는 경우에만 적용할 수 있습니다. 2. 미분성: 극한을 계산할 때 해당 지점에서 분자와 분모가 모두 미분 가능해야 합니다.3. 반복 적용: 첫 번째 미분 후에도 여전히 불확정성이 발생하는 경우 로피탈의 정리를 반복적으로 적용할 수 있습니다. 로피탈 정리의 예
예 1: ( lim_{x ~ 0} frac{sin(x)}{x} )1. 불확정 여부를 확인하세요: ( sin(0) = 0 ), ( x = 0 ), 따라서 0/0 형식입니다. 로피탈의 정리를 적용할 수 있습니다. 2. 분자와 분모 미분: – ( f(x) = sin(x) )의 미분은 ( f'(x) = cos(x) ) – ( g(x) = x )의 미분은 ( g'( x) = 1 )3. 극한을 다시 찾으세요: ( lim_{x to 0} frac{cos(x)}{1} = cos(0) = 1 )4. 결론: ( lim_{x ~ 0} frac{sin(x)}{x} = 1 )
예시 2: ( lim_{x ~ 0} frac{e^x – 1}{x} )1. 불확정 검사: ( e^x – 1 ~ 0 ) 및 ( x ~ 0 ), 따라서 0/0 형식입니다. 로피탈의 정리를 적용할 수 있습니다.2. 분자와 분모 미분: – ( f(x) = e^x – 1 )의 도함수는 ( f'(x) = e^x )입니다. – ( g(x) = x )의 도함수는 ( g'( x) = 1 )3. 극한을 다시 찾으세요: ( lim_{x to 0} frac{e^x}{1} = e^0 = 1 )4. 결론: ( lim_{x ~ 0} frac{e^x – 1}{x} = 1 )예 3: ( lim_{x ~ infty} frac{ln(x)}{x} )1. 불확정 검사: ( ln(x) 에서 infty ), ( x 에서 infty ), 따라서 무한/무한 형식입니다. 로피탈의 정리를 적용할 수 있습니다.2. 분자와 분모 미분: – ( f(x) = ln(x) )의 도함수는 ( f'(x) = frac{1}{x} ) – ( g(x) = x )의 도함수는 ( g'(x) = 1)3. 한계를 다시 찾으세요: ( lim_{x to infty} frac{frac{1}{x}}{1} = lim_{x to infty} frac{1}{x} = 0 )4. 결론: ( lim_{x ~ infty} frac{ln(x)}{x} = 0 )
로피탈 정리의 사용
극한 계산: 로피탈의 정리는 주로 극한을 찾는 문제에 유용합니다. 미분을 사용하면 불확정성을 해결할 수 있으므로 함수의 극한을 더 쉽게 계산할 수 있습니다. 수학적 분석: 함수의 성장률을 비교하거나 미분성을 분석할 때 중요한 역할을 합니다. 실제 적용: 로피탈의 정리는 물리학, 공학, 경제학 등 다양한 분야의 모델링 및 최적화 문제를 해결하는 데 사용됩니다. 로피탈의 정리에 대한 참고 사항
1. 반복 적용이 필요합니다. 한 번의 차별화 후에도 불규칙한 모양이 여전히 남아 있을 수 있습니다. 이 경우 차별화를 여러 번 반복해야 할 수도 있습니다. 2. 적용 조건을 확인하세요. 로피탈의 정리는 부정확한 상황에만 적용되며, 분자와 분모는 미분 가능해야 합니다. 따라서 사용 전 반드시 조건을 확인하시기 바랍니다.3. 극한의 존재: 로피탈의 정리를 적용한 후에도 극한이 존재하지 않거나 정의되지 않은 경우가 있을 수 있습니다. 이 경우 다른 방법을 사용해야 할 수도 있습니다.
#로피탈#수학 함수